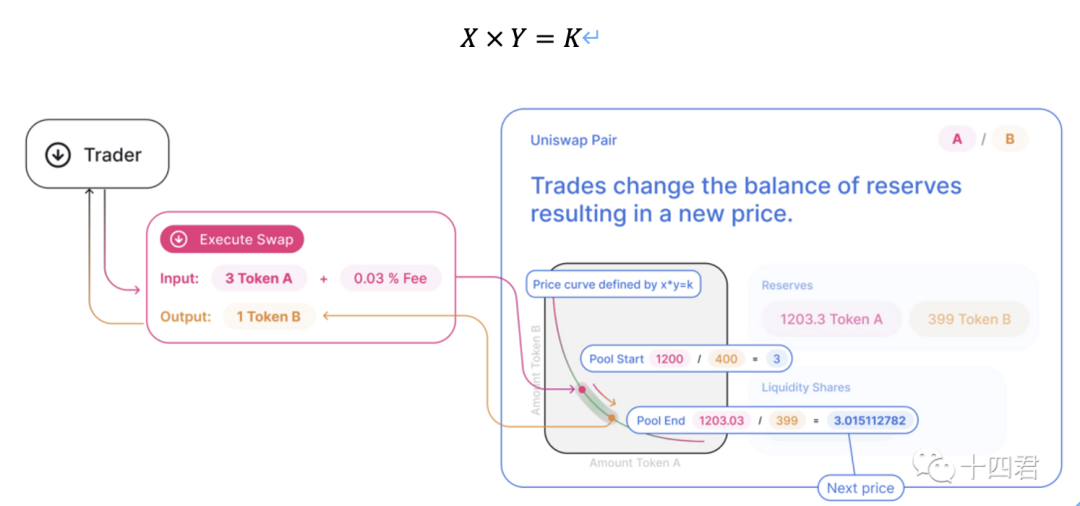
 AMM机制简介可阅读:一文讲清-NFT市场新秀SudoSwap的AMM机制-创新挑战与局限
部分公式中虚线系公式编辑器误操作,无实际意义
如需word源文档可在公众号后台回复“无常损失”获取
Part 1: 计算初始持有价值假定我持有若干e0(ETH) 以及若干t0(Token),初始两者价值相等,如 1 e0 = 10 t0,用公式表达其token的价格(用ETH本位计)则p0为:
AMM机制简介可阅读:一文讲清-NFT市场新秀SudoSwap的AMM机制-创新挑战与局限
部分公式中虚线系公式编辑器误操作,无实际意义
如需word源文档可在公众号后台回复“无常损失”获取
Part 1: 计算初始持有价值假定我持有若干e0(ETH) 以及若干t0(Token),初始两者价值相等,如 1 e0 = 10 t0,用公式表达其token的价格(用ETH本位计)则p0为:
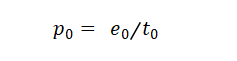 则我持有的总价值(用ETH计)等于数量*价格为:
则我持有的总价值(用ETH计)等于数量*价格为:
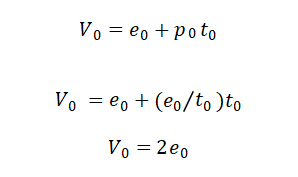 如果未进行Uniswap注入Lp的行为,则未来即使token对比Eth的价值变动,产生了新的价格,则我介时的资产总值VH为:
如果未进行Uniswap注入Lp的行为,则未来即使token对比Eth的价值变动,产生了新的价格,则我介时的资产总值VH为:
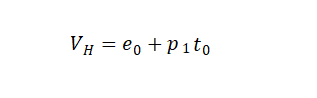 Part 2:为UniSwap注入流动性我们可以将ETH和代币两者按一定比例注入流动性,这里方便计算假定为按总值各占50%的注入,流动性池会给我们Lp的凭证,如10个LpToken用于证明我们占据当前总流动性的分红权益股份。由于恒积公式,只有注入和抽离LP会改变K值(本文中均不算手续费收入)
Part 2:为UniSwap注入流动性我们可以将ETH和代币两者按一定比例注入流动性,这里方便计算假定为按总值各占50%的注入,流动性池会给我们Lp的凭证,如10个LpToken用于证明我们占据当前总流动性的分红权益股份。由于恒积公式,只有注入和抽离LP会改变K值(本文中均不算手续费收入)
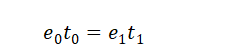 所以可以推导出计算当前e1的数量公式:
所以可以推导出计算当前e1的数量公式:
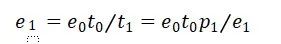 最终
最终
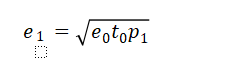 如此综合计算我们可以提取的流动性价值VU是
如此综合计算我们可以提取的流动性价值VU是
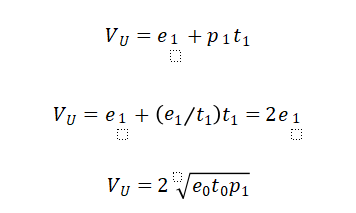 此处得出VU的将构成后续无常损失部分的被减数,因此特地为VU推导了上诉的两个采用e1以及不采用e1的公式
Part 3:无常损失公式推导依据Part1 我们得出了保持持有当前token的价值VH,
依据Part2 我们得出了不用持有而是投入Uniswap做LP的总价值VU,
显而易见:Divergence loss(无常损失或者发散损失)应该是VD
此处得出VU的将构成后续无常损失部分的被减数,因此特地为VU推导了上诉的两个采用e1以及不采用e1的公式
Part 3:无常损失公式推导依据Part1 我们得出了保持持有当前token的价值VH,
依据Part2 我们得出了不用持有而是投入Uniswap做LP的总价值VU,
显而易见:Divergence loss(无常损失或者发散损失)应该是VD
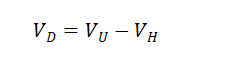 由于价值涨跌应该依据其对于原始价值的比值,所以我们把等式两边都除以VH
由于价值涨跌应该依据其对于原始价值的比值,所以我们把等式两边都除以VH
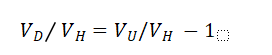 此处带入上文Part1和2结论中的VH与VU详细公式
此处带入上文Part1和2结论中的VH与VU详细公式
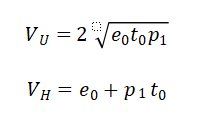 所以无常损失率VD/VH 为:
所以无常损失率VD/VH 为:
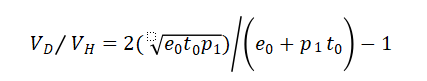 这时最关键的一步,无常损失发生在有价格差的两个时间段上,所以我们来带入价格的变化率R,其等于两个时间的价格相除
这时最关键的一步,无常损失发生在有价格差的两个时间段上,所以我们来带入价格的变化率R,其等于两个时间的价格相除
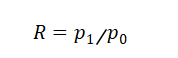 结合Part1中的公式
结合Part1中的公式
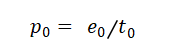 所以R也等于
所以R也等于
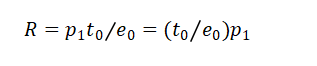 结合无常损失率VD/VH 我们将核心部分都乘以e0来形成只有R的最终公式
结合无常损失率VD/VH 我们将核心部分都乘以e0来形成只有R的最终公式
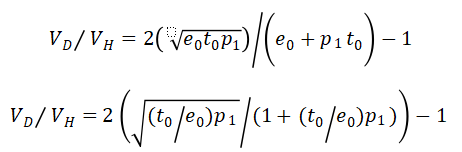 这样则可以化简出只有R来表示的无常损失率
这样则可以化简出只有R来表示的无常损失率
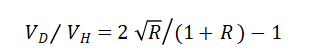 由于最终无常损失率值和R值有关系,则也意味着只要R有变动,无论增加还是减少,都将产生无常损失,并且按倍数衡量是一个对等的数值
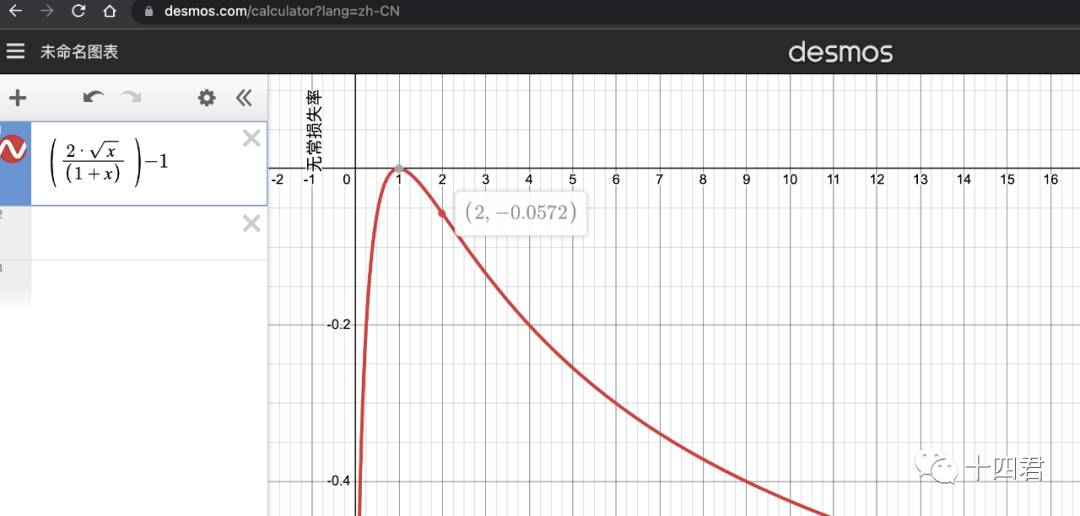
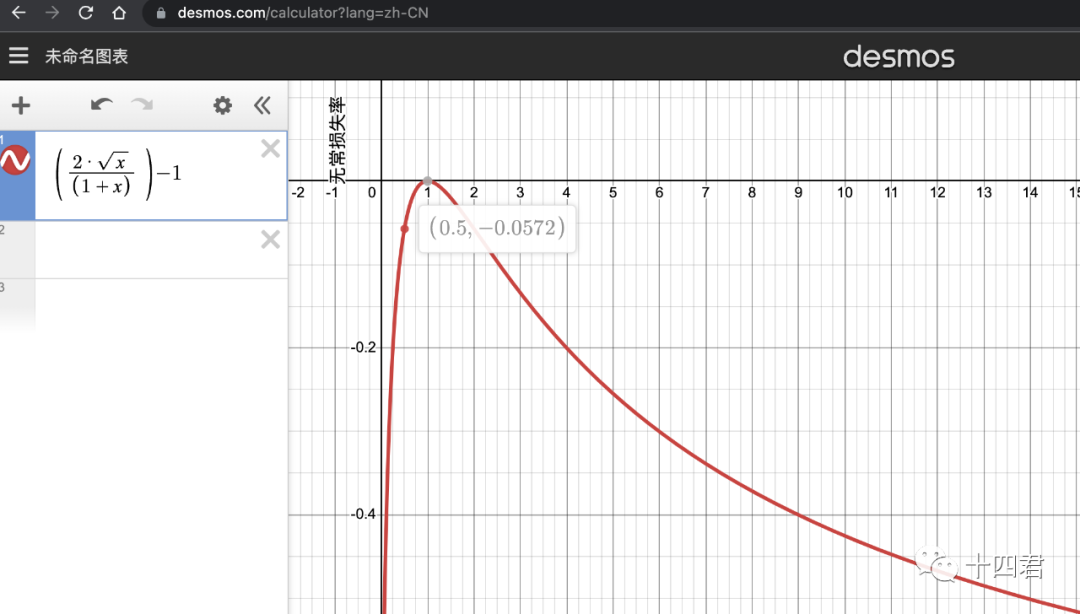
Part 4 图表化无常损失公式我们可以通过绘图工具来呈现这个公式的结果,虽然下图看似是一个非对称的曲线,但实际上是对称的,因为他是一个相对的倍率,即对于原价值的1ETH=100Dai而言,跌到1ETH=50Dai是下跌1倍,等于涨到1ETH=200Dai则是上涨1倍,其无常损失是相同的均为5.72%
由于最终无常损失率值和R值有关系,则也意味着只要R有变动,无论增加还是减少,都将产生无常损失,并且按倍数衡量是一个对等的数值
Part 4 图表化无常损失公式我们可以通过绘图工具来呈现这个公式的结果,虽然下图看似是一个非对称的曲线,但实际上是对称的,因为他是一个相对的倍率,即对于原价值的1ETH=100Dai而言,跌到1ETH=50Dai是下跌1倍,等于涨到1ETH=200Dai则是上涨1倍,其无常损失是相同的均为5.72%
 如何理解无常损失?
无常是什么意思?首先他是命名不恰当,之前选择“无常”( impermanent loss)这个词是因为如果价格背离被逆转,那么由于价格背离造成的损失也会被逆转,后来更多的文章会采用(divergence loss)来描述他。
无常损失在何时发生?如果价格回到与流动性提供者增加流动性时相同的价值,这种损失就会消失。这种损失只有在流动性提供者撤回其流动性时才会实现,并且是基于存款和取款之间的价格差异
无常损失会超过导致LP入不敷出吗?流动性提供者的实际回报,其实是价格差异造成的背离损失与交易所交易的累计费用之间的平衡。
如何理解无常损失?
无常是什么意思?首先他是命名不恰当,之前选择“无常”( impermanent loss)这个词是因为如果价格背离被逆转,那么由于价格背离造成的损失也会被逆转,后来更多的文章会采用(divergence loss)来描述他。
无常损失在何时发生?如果价格回到与流动性提供者增加流动性时相同的价值,这种损失就会消失。这种损失只有在流动性提供者撤回其流动性时才会实现,并且是基于存款和取款之间的价格差异
无常损失会超过导致LP入不敷出吗?流动性提供者的实际回报,其实是价格差异造成的背离损失与交易所交易的累计费用之间的平衡。
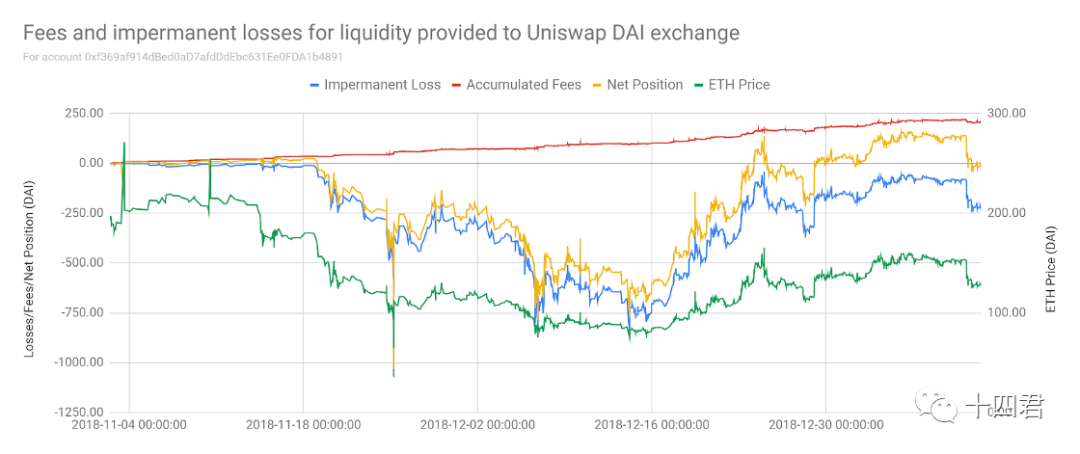 如上图,该账户自成为LP以来,与仅持有原始资金相比,该账户一直处于净负头寸(黄线)。这是由于在此期间 ETH 价格变动(绿线)造成的巨大背离损失(蓝线)。然而,自始至终总费用一直在稳步累积(红线)。随着 ETH 价格接近提供流动性的价格,大部分损失会被扭转。
无常损失究竟来源何处?向市场提供流动性做LP,即成为做市商,实际上是和市场中的用户做对手盘。而 AMM(自动化做市商)是被动的和市场中的用户做对手盘,即当市场中大部分人看好 ETH 的后续市场,则会用 DAI 买入 ETH,你的流动性池子会被动的增加 DAI 而减少 ETH。
所以,提供流动性就代表了总是和市场做反向的操作,总是倾向去持有更多的弱势资产(当 ETH 上涨为强势资产,DAI 就是弱势资产)。于是当 ETH 上涨,你的流动性会不断提前抛出 ETH,而拿到更多的 DAI,这些被提前抛出的 ETH 就成了无常损失的来源,即这个时候无常损失可以理解为你在 ETH 上的踏空损失,或者是被外部套利者拿走了池内的价值。
相关资料
https://uniswap.org/whitepaper.pdf
https://pintail.medium.com/understanding-uniswap-returns-cc593f3499ef
https://pintail.medium.com/uniswap-a-good-deal-for-liquidity-providers-104c0b6816f2
https://hackmd.io/@HaydenAdams/HJ9jLsfTz
https://github.com/Dapp-Learning-DAO/Dapp-Learning/blob/main/basic/13-decentralized-exchange/uniswap-v1-like/README.md
如上图,该账户自成为LP以来,与仅持有原始资金相比,该账户一直处于净负头寸(黄线)。这是由于在此期间 ETH 价格变动(绿线)造成的巨大背离损失(蓝线)。然而,自始至终总费用一直在稳步累积(红线)。随着 ETH 价格接近提供流动性的价格,大部分损失会被扭转。
无常损失究竟来源何处?向市场提供流动性做LP,即成为做市商,实际上是和市场中的用户做对手盘。而 AMM(自动化做市商)是被动的和市场中的用户做对手盘,即当市场中大部分人看好 ETH 的后续市场,则会用 DAI 买入 ETH,你的流动性池子会被动的增加 DAI 而减少 ETH。
所以,提供流动性就代表了总是和市场做反向的操作,总是倾向去持有更多的弱势资产(当 ETH 上涨为强势资产,DAI 就是弱势资产)。于是当 ETH 上涨,你的流动性会不断提前抛出 ETH,而拿到更多的 DAI,这些被提前抛出的 ETH 就成了无常损失的来源,即这个时候无常损失可以理解为你在 ETH 上的踏空损失,或者是被外部套利者拿走了池内的价值。
相关资料
https://uniswap.org/whitepaper.pdf
https://pintail.medium.com/understanding-uniswap-returns-cc593f3499ef
https://pintail.medium.com/uniswap-a-good-deal-for-liquidity-providers-104c0b6816f2
https://hackmd.io/@HaydenAdams/HJ9jLsfTz
https://github.com/Dapp-Learning-DAO/Dapp-Learning/blob/main/basic/13-decentralized-exchange/uniswap-v1-like/README.md










